一致性HASH算法实现

2022-09-29

一致性哈希算法是分布式系统中常用的算法。一致性哈希算法解决了普通余数 Hash 算法伸缩性差的问题，可以保证在上线、下线服务器的情况下尽量有多的请求命中原来路由到的服务器。

一致性 hash 算法解决了分布式环境下机器增加或者减少时，简单的取模运算无法获取较高命中率的问题。通过虚拟节点的使用，一致性 hash 算法可以均匀分担机器的负载，使得这一算法更具现实的意义。正因如此，一致性 hash 算法被广泛应用于分布式系统中。

一、一致性 Hash(Consistent Hashing) 原理剖析

引入

在业务开发中，我们常把数据持久化到数据库中。如果需要读取这些数据，除了直接从数据库中读取外，为了减轻数据库的访问压力以及提高访问速度，我们更多地引入缓存来对数据进行存取。读取数据的过程一般为：

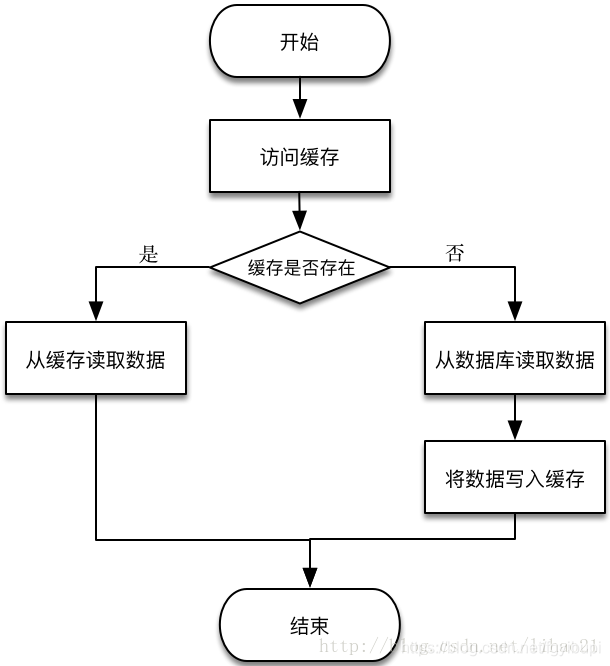
对于分布式缓存，不同机器上存储不同对象的数据。为了实现这些缓存机器的负载均衡，可以使用式子 1 来定位对象缓存的存储机器：

1	m = hash(o) mod n ——式子1

其中，o 为对象的名称，n 为机器的数量，m 为机器的编号，hash 为一 hash 函数。图 2 中的负载均衡器（load balancer）正是使用式子 1 来将客户端对不同对象的请求分派到不同的机器上执行，例如，对于对象 o，经过式子 1 的计算，得到 m 的值为 3，那么所有对对象 o 的读取和存储的请求都被发往机器 3 执行。

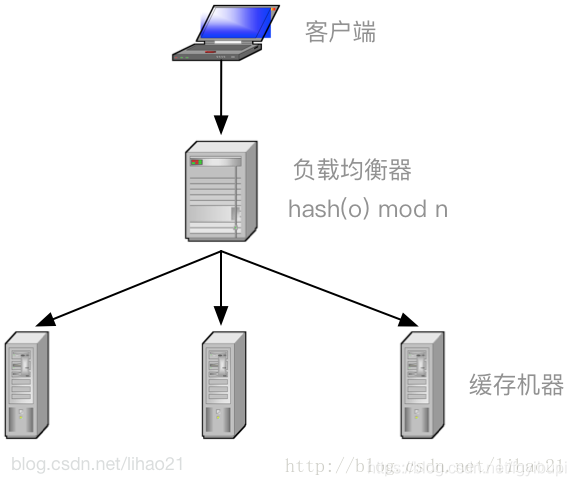
式子 1 在大部分时候都可以工作得很好，然而，当机器需要扩容或者机器出现宕机的情况下，事情就比较棘手了。
当机器扩容，需要增加一台缓存机器时，负载均衡器使用的式子变成：

1	m = hash(o) mod (n + 1) ——式子2

当机器宕机，机器数量减少一台时，负载均衡器使用的式子变成：

1	m = hash(o) mod (n - 1) ——式子3

我们以机器扩容的情况为例，说明简单的取模方法会导致什么问题。假设机器由 3 台变成 4 台，对象 o1 由式子 1 计算得到的 m 值为 2，由式子 2 计算得到的 m 值却可能为 0，1，2，3（一个 3t + 2 的整数对 4 取模，其值可能为 0，1，2，3，读者可以自行验证），大约有 75%（3/4) 的可能性出现缓存访问不命中的现象。随着机器集群规模的扩大，这个比例线性上升。当 99 台机器再加入 1 台机器时，不命中的概率是 99%（99/100）。这样的结果显然是不能接受的，因为这会导致数据库访问的压力陡增，严重情况，还可能导致数据库宕机。

一致性 hash 算法正是为了解决此类问题的方法，它可以保证当机器增加或者减少时，对缓存访问命中的概率影响减至很小。下面我们来详细说一下一致性 hash 算法的具体过程。

一致性 Hash 环

一致性 hash 算法通过一个叫作一致性 hash 环的数据结构实现。这个环的起点是 0，终点是 2^32 - 1，并且起点与终点连接，环的中间的整数按逆时针分布，故这个环的整数分布范围是 [0, 2^32-1]，如下图 3 所示：

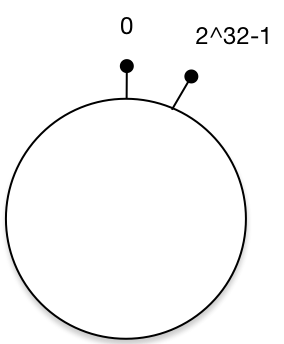
将对象放置到 Hash 环
假设现在我们有 4 个对象，分别为 o1，o2，o3，o4，使用 hash 函数计算这 4 个对象的 hash 值（范围为 0 ~ 2^32-1）:

hash(o1) = m1 
hash(o2) = m2 
hash(o3) = m3 
hash(o4) = m4

把 m1，m2，m3，m4 这 4 个值放置到 hash 环上，得到如下图 4：

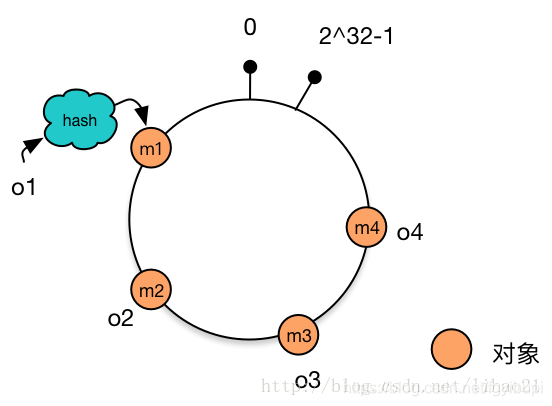
将机器放置到 Hash 环
使用同样的 hash 函数，我们将机器也放置到 hash 环上。假设我们有三台缓存机器，分别为 c1，c2，c3，使用 hash 函数计算这 3 台机器的 hash 值：

1
2
3

hash(c1) = t1 
hash(c2) = t2 
hash(c3) = t3

把 t1，t2，t3 这 3 个值放置到 hash 环上，得到如下图 5：

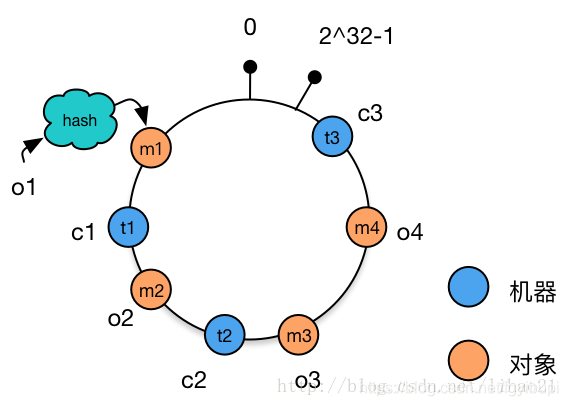
为对象选择机器

将对象和机器都放置到同一个 hash 环后，在 hash 环上顺时针查找距离这个对象的 hash 值最近的机器，即是这个对象所属的机器。
例如，对于对象 o2，顺序针找到最近的机器是 c1，故机器 c1 会缓存对象 o2。而机器 c2 则缓存 o3，o4，机器 c3 则缓存对象 o1。

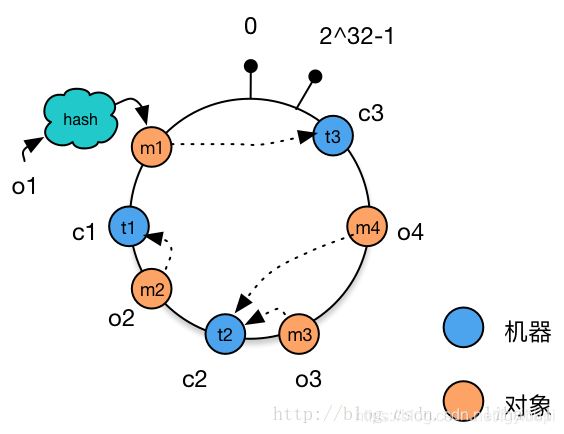
处理机器增减的情况

对于线上的业务，增加或者减少一台机器的部署是常有的事情。
例如，增加机器 c4 的部署并将机器 c4 加入到 hash 环的机器 c3 与 c2 之间。这时，只有机器 c3 与 c4 之间的对象需要重新分配新的机器。对于我们的例子，只有对象 o4 被重新分配到了 c4，其他对象仍在原有机器上。如图 7 所示：

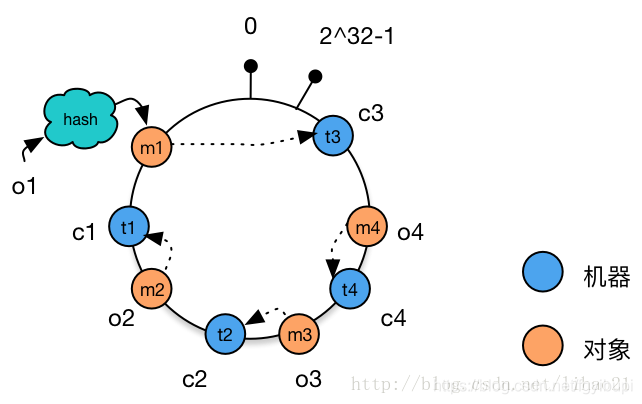
如上文前面所述，使用简单的求模方法，当新添加机器后会导致大部分缓存失效的情况，使用一致性 hash 算法后这种情况则会得到大大的改善。前面提到 3 台机器变成 4 台机器后，缓存命中率只有 25%（不命中率 75%）。而使用一致性 hash 算法，理想情况下缓存命中率则有 75%，而且，随着机器规模的增加，命中率会进一步提高，99 台机器增加一台后，命中率达到 99%，这大大减轻了增加缓存机器带来的数据库访问的压力。

再例如，将机器 c1 下线（当然，也有可能是机器 c1 宕机），这时，只有原有被分配到机器 c1 对象需要被重新分配到新的机器。对于我们的例子，只有对象 o2 被重新分配到机器 c3，其他对象仍在原有机器上。如图 8 所示：

虚拟节点

上面提到的过程基本上就是一致性 hash 的基本原理了，不过还有一个小小的问题。新加入的机器 c4 只分担了机器 c2 的负载，机器 c1 与 c3 的负载并没有因为机器 c4 的加入而减少负载压力。如果 4 台机器的性能是一样的，那么这种结果并不是我们想要的。
为此，我们引入虚拟节点来解决负载不均衡的问题。
将每台物理机器虚拟为一组虚拟机器，将虚拟机器放置到 hash 环上，如果需要确定对象的机器，先确定对象的虚拟机器，再由虚拟机器确定物理机器。
说得有点复杂，其实过程也很简单。

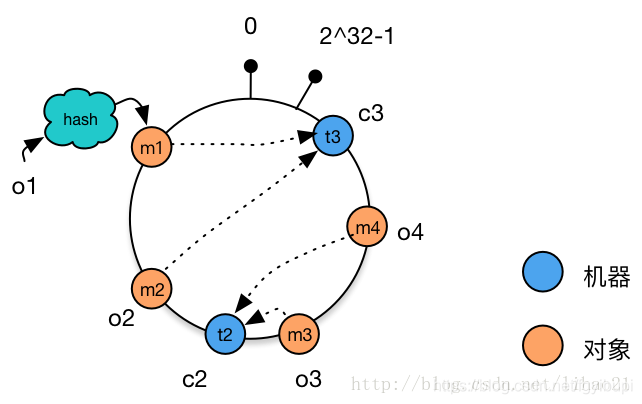
还是使用上面的例子，假如开始时存在缓存机器 c1，c2，c3，对于每个缓存机器，都有 3 个虚拟节点对应，其一致性 hash 环结构如图 9 所示：

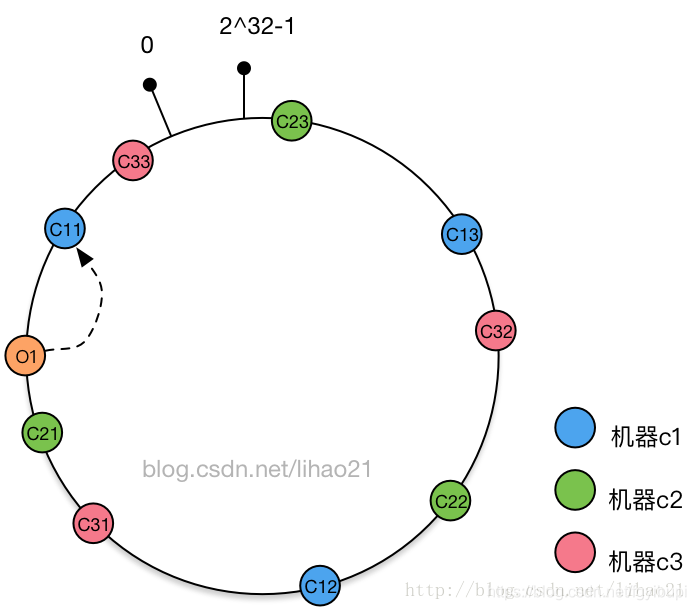
假设对于对象 o1，其对应的虚拟节点为 c11，而虚拟节点 c11 对象缓存机器 c1，故对象 o1 被分配到机器 c1 中。

新加入缓存机器 c4，其对应的虚拟节点为 c41，c42，c43，将这三个虚拟节点添加到 hash 环中，得到的 hash 环结构如图 10 所示：

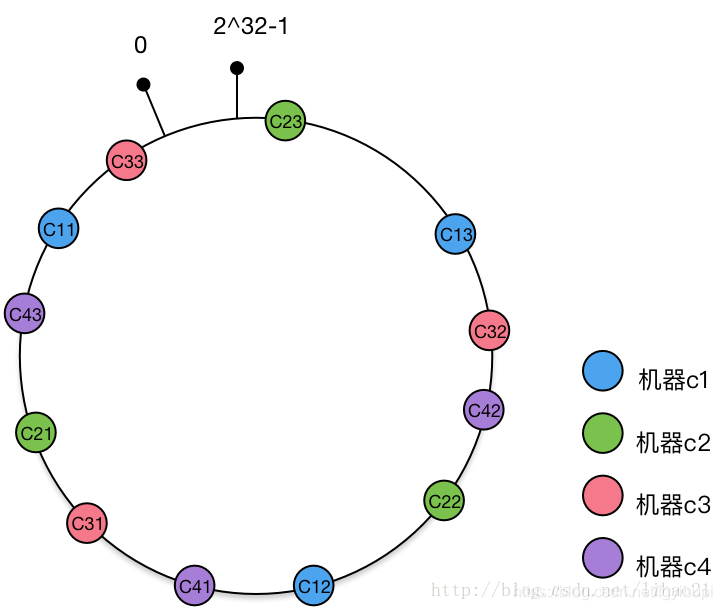
新加入的缓存机器 c4 对应一组虚拟节点 c41，c42，c43，加入到 hash 环后，影响的虚拟节点包括 c31，c22，c11（顺时针查找到第一个节点），而这 3 个虚拟节点分别对应机器 c3，c2，c1。即新加入的一台机器，同时影响到原有的 3 台机器。理想情况下，新加入的机器平等地分担了原有机器的负载，这正是虚拟节点带来的好处。而且新加入机器 c4 后，只影响 25%（1/4）对象分配，也就是说，命中率仍然有 75%，这跟没有使用虚拟节点的一致性 hash 算法得到的结果是相同的。

二、一致性 hash 算法的 Java 实现

1、不带虚拟节点的

package hash;
 
import java.util.SortedMap;
import java.util.TreeMap;
 
/**
 * 不带虚拟节点的一致性Hash算法
 */
public class ConsistentHashingWithoutVirtualNode {
 
	//待添加入Hash环的服务器列表
	private static String[] servers = { "192.168.0.0:111", "192.168.0.1:111",
			"192.168.0.2:111", "192.168.0.3:111", "192.168.0.4:111" };
 
	//key表示服务器的hash值，value表示服务器
	private static SortedMap<Integer, String> sortedMap = new TreeMap<Integer, String>();
 
	//程序初始化，将所有的服务器放入sortedMap中
	static {
		for (int i=0; i<servers.length; i++) {
			int hash = getHash(servers[i]);
			System.out.println("[" + servers[i] + "]加入集合中, 其Hash值为" + hash);
			sortedMap.put(hash, servers[i]);
		}
		System.out.println();
	}
 
	//得到应当路由到的结点
	private static String getServer(String key) {
		//得到该key的hash值
		int hash = getHash(key);
		//得到大于该Hash值的所有Map
		SortedMap<Integer, String> subMap = sortedMap.tailMap(hash);
		if(subMap.isEmpty()){
			//如果没有比该key的hash值大的，则从第一个node开始
			Integer i = sortedMap.firstKey();
			//返回对应的服务器
			return sortedMap.get(i);
		}else{
			//第一个Key就是顺时针过去离node最近的那个结点
			Integer i = subMap.firstKey();
			//返回对应的服务器
			return subMap.get(i);
		}
	}
	
	//使用FNV1_32_HASH算法计算服务器的Hash值,这里不使用重写hashCode的方法，最终效果没区别
	private static int getHash(String str) {
		final int p = 16777619;
		int hash = (int) 2166136261L;
		for (int i = 0; i < str.length(); i++)
			hash = (hash ^ str.charAt(i)) * p;
		hash += hash << 13;
		hash ^= hash >> 7;
		hash += hash << 3;
		hash ^= hash >> 17;
		hash += hash << 5;
 
		// 如果算出来的值为负数则取其绝对值
		if (hash < 0)
			hash = Math.abs(hash);
		return hash;
		}
 
	public static void main(String[] args) {
		String[] keys = {"太阳", "月亮", "星星"};
		for(int i=0; i<keys.length; i++)
			System.out.println("[" + keys[i] + "]的hash值为" + getHash(keys[i])
					+ ", 被路由到结点[" + getServer(keys[i]) + "]");
	}
}

执行结果：

[192.168.0.0:111]加入集合中, 其Hash值为575774686
[192.168.0.1:111]加入集合中, 其Hash值为8518713
[192.168.0.2:111]加入集合中, 其Hash值为1361847097
[192.168.0.3:111]加入集合中, 其Hash值为1171828661
[192.168.0.4:111]加入集合中, 其Hash值为1764547046

[太阳]的hash值为1977106057, 被路由到结点[192.168.0.1:111]
[月亮]的hash值为1132637661, 被路由到结点[192.168.0.3:111]
[星星]的hash值为880019273, 被路由到结点[192.168.0.3:111]

2、带虚拟节点的

package hash;
 
import java.util.LinkedList;
import java.util.List;
import java.util.SortedMap;
import java.util.TreeMap;
 
import org.apache.commons.lang.StringUtils;
 
/**
  * 带虚拟节点的一致性Hash算法
  */
 public class ConsistentHashingWithoutVirtualNode {
 
     //待添加入Hash环的服务器列表
     private static String[] servers = {"192.168.0.0:111", "192.168.0.1:111", "192.168.0.2:111",
             "192.168.0.3:111", "192.168.0.4:111"};
     
     //真实结点列表,考虑到服务器上线、下线的场景，即添加、删除的场景会比较频繁，这里使用LinkedList会更好
     private static List<String> realNodes = new LinkedList<String>();
     
     //虚拟节点，key表示虚拟节点的hash值，value表示虚拟节点的名称
     private static SortedMap<Integer, String> virtualNodes = new TreeMap<Integer, String>();
             
     //虚拟节点的数目，这里写死，为了演示需要，一个真实结点对应5个虚拟节点
     private static final int VIRTUAL_NODES = 5;
     
     static{
         //先把原始的服务器添加到真实结点列表中
         for(int i=0; i<servers.length; i++)
             realNodes.add(servers[i]);
         
         //再添加虚拟节点，遍历LinkedList使用foreach循环效率会比较高
         for (String str : realNodes){
             for(int i=0; i<VIRTUAL_NODES; i++){
                 String virtualNodeName = str + "&&VN" + String.valueOf(i);
                 int hash = getHash(virtualNodeName);
                 System.out.println("虚拟节点[" + virtualNodeName + "]被添加, hash值为" + hash);
                 virtualNodes.put(hash, virtualNodeName);
             }
         }
         System.out.println();
     }
     
     //使用FNV1_32_HASH算法计算服务器的Hash值,这里不使用重写hashCode的方法，最终效果没区别
     private static int getHash(String str){
         final int p = 16777619;
         int hash = (int)2166136261L;
         for (int i = 0; i < str.length(); i++)
             hash = (hash ^ str.charAt(i)) * p;
         hash += hash << 13;
         hash ^= hash >> 7;
         hash += hash << 3;
         hash ^= hash >> 17;
         hash += hash << 5;
         
         // 如果算出来的值为负数则取其绝对值
         if (hash < 0)
             hash = Math.abs(hash);
         return hash;
     }
     
     //得到应当路由到的结点
     private static String getServer(String key){
        //得到该key的hash值
         int hash = getHash(key);
         // 得到大于该Hash值的所有Map
         SortedMap<Integer, String> subMap = virtualNodes.tailMap(hash);
         String virtualNode;
         if(subMap.isEmpty()){
            //如果没有比该key的hash值大的，则从第一个node开始
            Integer i = virtualNodes.firstKey();
            //返回对应的服务器
            virtualNode = virtualNodes.get(i);
         }else{
            //第一个Key就是顺时针过去离node最近的那个结点
            Integer i = subMap.firstKey();
            //返回对应的服务器
            virtualNode = subMap.get(i);
         }
         //virtualNode虚拟节点名称要截取一下
         if(StringUtils.isNotBlank(virtualNode)){
             return virtualNode.substring(0, virtualNode.indexOf("&&"));
         }
         return null;
     }
     
     public static void main(String[] args){
         String[] keys = {"太阳", "月亮", "星星"};
         for(int i=0; i<keys.length; i++)
             System.out.println("[" + keys[i] + "]的hash值为" +
                     getHash(keys[i]) + ", 被路由到结点[" + getServer(keys[i]) + "]");
     }
 }